Disclaimer: I received a FREE copy of this product through the HOMESCHOOL REVIEW CREW in exchange for my honest review. I was not required to write a positive review nor was I compensated in any other way.
I had the pleasure of reviewing Math Galaxy through the various math apps they have available as well as their downloadable math ebooks. Math Galaxy is a math curriculum available for grades 3 math all the way through algebra math along with SAT math studies.
When I showed the math apps and ebooks to my kids, they were excited to have a math program on a tablet that they can take anywhere with them. Instead of YouTube videos, my kids jumped straight to Math Galaxy’s various math riddles and balloon games!
Whether you already have a math curriculum for your homeschool, as we do, or you purchase of the programs out there, think about how much effort you put forward in sitting down and teaching your kids the math concepts they need. Probably a lot of time, yes?
Quick Navigation
Math Galaxy Review
Many parents I have talked to will admit that math is the determining factor for their homeschool’s success or demise! Pretty scary to chalk up your entire homeschool by teaching math to your child successfully! Yet, homeschool parents know that math is one of the most important subjects to teach in homeschool and at the same time one of the most challenging.
When a math curriculum presents itself, it is up to the parent to both read the teaching instructions and understand out to best present it to your child. Determining which curriculum program to go with and how to best present it to your child in order to satisfy your own scope and sequence for your kiddos is a must for any homeschool family.
If you do a google search online you will come across an overwhelming number of math curricula available! Some are teacher intensive while others are forcing independence to the students. Some address kinesthetic learners while others address visual learners. And some still push the parents to creatively think about their own way to present the teaching methods to their children’s’ learning styles.
It is of little wonder why a math curriculum is one of the most challenging and ever-changing curricula in any homeschool. It usually takes quite a bit of time to find a math curriculum that fits your family’s needs as well as your children’s multiple learning styles. One program may work with one child and not the other.
Additionally, your child may need extra time and attention on certain concepts that they’re just not getting, and that’s where your extra time goes as well – to the success of your child’s math skills.
Think about how much time you can save by supplementing some of those math concepts with extra help. Or better yet, by having focused concepts a click away that adds not only understanding to your child’s math skills but also adds a giggle!
What if math was…dare I say…fun?!
Enter: Math Galaxy
Math Galaxy solves the homeschool math overwhelm for your math studies by giving you an option to take your math on the go via apps as well as giving your the downloadable and printable options for ebooks. This means that when your child needs to focus a bit more on a math concept, open up a math app on your way to the store, and let the math lesson unfold readily for your child, anytime, anywhere. This also means that this math curriculum can stand as its own pillar math program with the option of mastering one concept after another via ebooks!
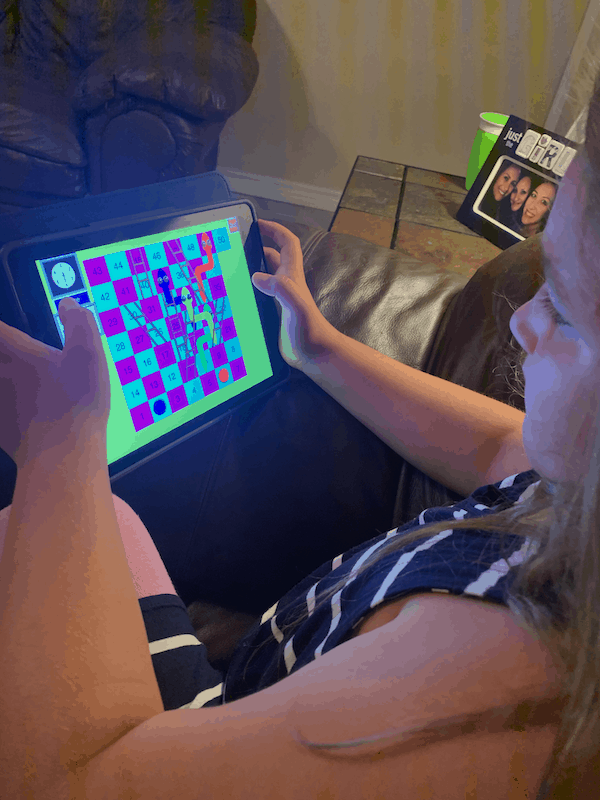
This math program has seriously saved me precious mama time, where it’s already limited enough as it is. With a tornado toddler running around, I try to find the best solutions to make things easier for me while at the same time successfully solving an issue. One of my issues was extra time and attention needed in order to nurture those pesky math concepts!
Math Galaxy has saved me hours so far of that mama time while serving as a math tutor to my kiddos! With award-winning homeschool math apps for iOS devices, Math Galaxy puts humor and giggles into a usually potentially monotonous situation! With math games and math riddles my children were eager to keep doing more math problems!
Fun and learning math? I’ll take it!
Using Math Galaxy is straightforward, practical, very affordable, and easy to understand. If you’re a homeschool mom with kids between the levels of grade 3 all the way through high school with a desire to add fun and games to your math curriculum, I can’t swear by Math Galaxy enough!
How to Use Math Galaxy
We received a couple of downloadable ebooks and a few downloadable apps for iOS to use in exchange for an honest review of the program. It is a digital curriculum product that you access through a link they send you to download the ebooks as well as apps you download to access via an iOS device, such as an iPad or iPhone. Once you download the ebooks, you print the concepts as you go, whether you want to print them via weekly lessons or via the concept as a whole.
I downloaded the ebooks I received and printed out per the concepts my children were struggling with the most. For my son, I received the Fractions ebook and for my daughter, I received the Whole Numbers bundle ebook.
The Math Fractions bundle has 8 separate ebooks/concepts with 40-70 pages each.

The Math Whole Numbers bundle has 11 separate ebooks/concepts with 40-70 pages.

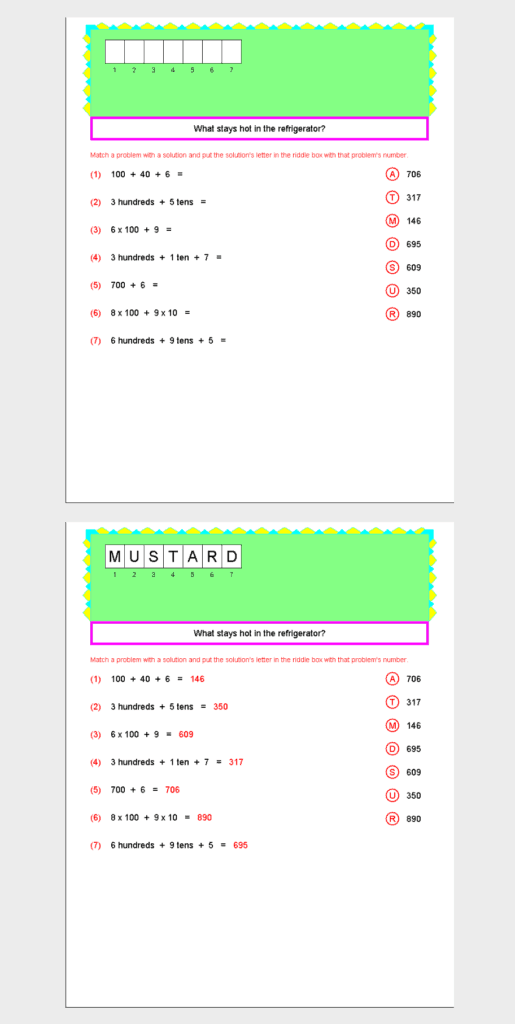
Each book has a table of contents, like this one for Adding & Subtracting Fractions:

We added Math Galaxy as a supplement to our current math curriculum. Each ebook within a bundle introduces a new math concept. You can print out the riddles and games as you go or, like us, print out a week’s worth to work into your daily morning warm-up.
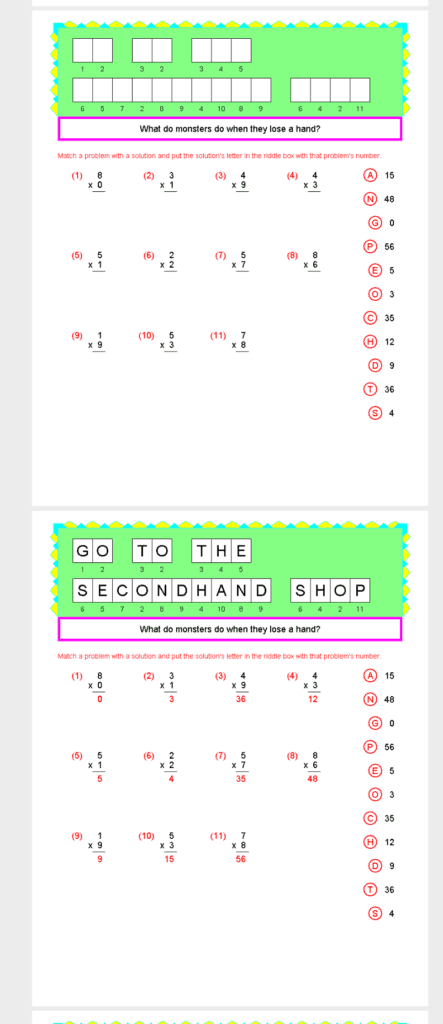
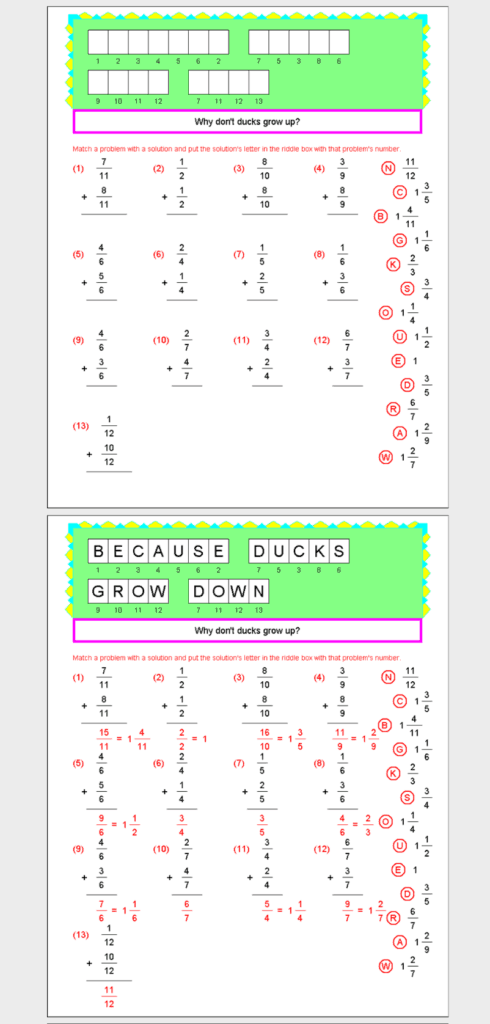
Every morning I add in a math concept before my kids even start school. It is usually a 1-2 sheet of paper and it’s the first thing they do before anything else and after their morning time routine. Each day is a new worksheet where it focuses on a math concept that they need extra practice on. This is where Math Galaxy really shines: the concepts work extremely well as their daily morning warm-up, especially since my kids are eager to solve the problems in order to figure out the riddles’ answers!
Although each page is its own riddle, you can merge these pages to make a day’s worth of math lessons. For example, you can group together several pages of digital multiplication into one day, where the kids will learn a new math concept and do a few pages of math riddles as practice.
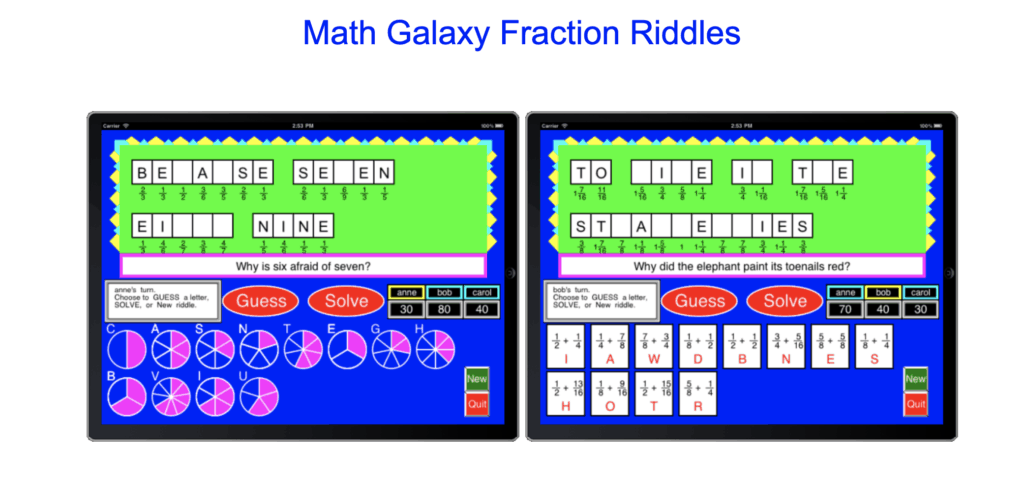
The riddles in the ebooks brought us some great discussions about the concepts at hand. For instance, every time my child finished a riddle they would come show me the question and answer that they were solving. It would bring about a few comments about the riddle and why the answer is what it is. To be honest, sometimes we didn’t understand why the answer was the answer, or the answer itself was a little corny, but overall we did enjoy working our way through the riddles to get to the answers.
Math Galaxy is a simple homeschool math curriculum to get into a rhythm with and once you begin your lessons you will soon get the hang of adding them into your daily homeschool. We began to look forward to our math warm-ups because both I and the kids knew it would “break the ice” to our new homeschool day and open our brains up to both fun and learning! That’s a winner in my book!
More Awesome Things About Math Galaxy
We travel a lot – or we run all over town all the time – which brings me to another exciting aspect of Math Galaxy: their downloadable apps! Not only did we receive a couple of ebooks to use in our homeschool, but we also received a few math apps too:
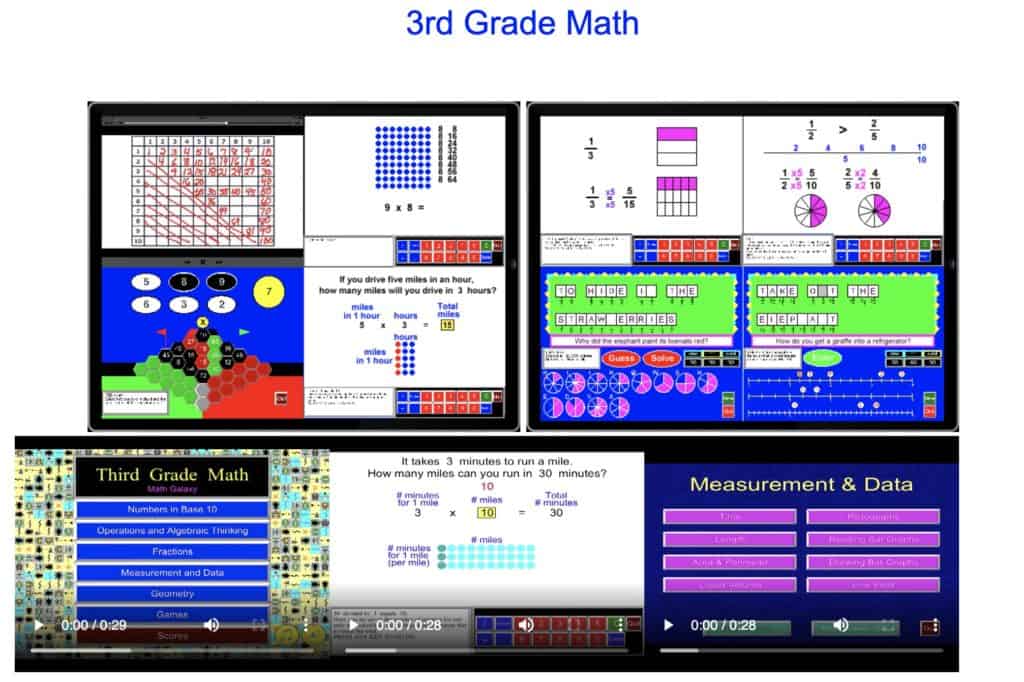
3rd Grade Math
4th Grade Math
Whole Number Riddles
Times Table Balloon Pop
Word Problems Fun
Every time we left the house or even had extra downtime at home, such as my toddler’s naptime that encouraged quiet time, my kids would grab the iPad and do math games from the Math Galaxy apps. I often witnessed them jumping to do the math games in the evening time as well. This is when all those discussions I mentioned would take place!

My kids would pick an app that I have available for them, a math concept that they wanted to pursue such as times tables, and that independent initiative itself gave them a sense of control over an otherwise seemingly-out-of-their-control subject. Math is hard, anyone will tell you that. Learning math usually means learning something you don’t know yet, so to work out a math problem – and getting it wrong – can lead to frustration.
This frustration didn’t happen with Math Galaxy. They enjoyed working out the riddles because they were math riddles and games! They didn’t take on the subject of mathematics as a completely serious venture because the math approach itself that Math Galaxy establishes is literally all fun and games. My kids simply worked out the math problems until they got them correct!
My Opinion: Math Galaxy Review
I found the entire curriculum laid out and structured as simple as it could be for a math curriculum, with a mastery approach to it as it bundles up the ebooks and apps into math concepts. Once a kiddo masters that concept, they move on to the next one. Because I already have the ebooks downloaded from a zip file, it was easy to see “what was next” according to their math scope and sequence.
If I had to pick a dislike about the product, it would be that, although the ebooks were fun, it does take a bit of colored ink if you were to print them out in colored ink. Even if you printed it out in black and white, you’d still use up a bit of black ink. The riddle bubbles to solve are at the top of the page, and the bubble itself is a solid color. I wasn’t thrilled about using up my ink, especially since the ink replacement cartridges can be so expensive just about anywhere.
I have to use ink in other subjects so to hoard it on math worksheets didn’t seem really fair. The good news is, I used the ebook worksheets as our daily warm-ups so I didn’t print out multiple pages of each concept for every day. I used 1-2 riddles (and didn’t print out the answer sheets) per day as warm-ups and that seemed sufficient for both satisfying their math warm-ups and using the curriculum itself.
With Math Galaxy set up as a fun game and riddle approach, my children were able to visually see and understand math concepts in a whole new manner. With a stronger grasp on their math concepts, my kids can seamlessly enter the next concept with confidence and ease. No more holes in their math skills!
Although Math Galaxy is set up for grades 3 and up, they just introduced their brand new Pre-K math app! I was able to retrieve this app as well, although I haven’t used it yet as both of my homeschool kids are upper elementary and my toddler is just 2. However, I’m looking forward to using this gentle approach to math for my toddler in just a few years! We really did enjoy how fun Math Galaxy made learning math!
Practical Product Details
Math Galaxy offers so many more apps and ebook bundles than I mentioned here! They have literally everything I can think of for math exposure from grade 3 all the way to algebra, and even beyond algebra for SAT studies. You can purchase the apps and ebook bundles separately or together as a bigger bundle. The ebooks will be downloadable to your email address and to access your newly purchased apps will be via code. Or you can purchase the apps one at a time through the iOS app store. Unfortunately, the apps are only available via iOS devices and not available through any other at the time of this writing.

Math Galaxy Review
Wrapping up this Math Galaxy review, I love how simple yet effective this math curriculum is, whether it be used as a supplement or you decide to make it your entire math curriculum. After downloading your ebook zip files and apps, you have a fun math curriculum that lightens the load of that stinky old “math overwhelm” feeling we all tend to get from time to time.
Now that you’re aware of some of the thrilling highlights of this fun math program, you are now fully-equipped to try Math Galaxy out yourself!
Be sure to visit the Homeschool Review Crew blog to read more reviews of Math Galaxy. My family loves this curriculum, and other families used it as well in exchange for an honest review, so be sure to check out their reviews by clicking on the banner!

- 55 Inspiring Mindfulness Quotes For Kids Every Mom Should Know - May 7, 2024
- 111 Best All-Time Middle School Movies List (In Categories!) - April 26, 2024
- Top 16 Indoor Games for Teens That Won’t Turn Your House into a War Zone - January 29, 2024















Thanks for the work you put into this.
If you’re concerned about printing costs for the eBooks, there are Google Slides for many of the eBooks that can be accessed from MathGalaxy.com or found at TeachersPayTeachers.com.
That sounds fantastic and would solve any printing costs concerns. Thanks so much for sharing that info. Do the slides cost extra or do they come with the ebooks, on TpT or on MathGalaxy.com?
Thanks for all the time that you put into this.
There are Google Slides for many of the Whole Number and Fraction eBooks that can be practiced on a computer, and more to come.
You can find links to them at MathGalaxy.com.
That sounds wonderful! Thanks for sharing that info. And it was quite our pleasure to use the Math Galaxy program. We appreciate the work that you put into making math fun and exciting!